← Back

Problem 3.2 Balanced Brackets

The balanced brackets problem is fundamental in validating nested structures in programming languages and markup documents, ensuring correct syntax and hierarchy. It is widely used in compilers, interpreters, and data structure manipulation to detect structural errors efficiently.

The Problem: Given a string consisting of a sequence of characters from: `{`, `}`, `[`, `]`, `(`, and `)`, determine if the brackets in the sequence are balanced or not.

A sequence of brackets is considered balanced if: every opening bracket has a corresponding closing bracket in the correct order of nesting.

Some examples

Some example strings and their status as either balanced or not balanced is given below.

"{([])}{}" is balanced
"{{[[(())]]}}" is balanced
"([{}])" is balanced
"" (empty string) is balanced

"([)]" is not balanced
"()]" is not balanced
"{([)]}" is not balanced

A method for the solution

At this point: attempt to solve this problem without looking at the following method. You'll notice that it becomes complicated to solve by scaning the list in the usual manner.

Using the list as a Stack

A stack is a data structure that follows the Last In, First Out (LIFO) principle, meaning the last item added is the first one removed. Think of it like stacking plates: you add a new plate on top, and when you take one off, you remove the topmost plate first.

In Python, a list can easily function as a stack. By using the append() method, we add items to the end of the list (the top of the stack). The pop() method removes the last item added, making it perfect for implementing stack behavior.

Checking balanced brackets with a stack

The gist of the method is this: scan the input one bracket at a time. If an opening bracket is encountered, push it into the stack. If a closing bracket is encountered, check the bracket added last (at the top of the stack); if the opening and closing brackets match, remove the opening bracket and continue to the next bracket in the input. In case of a mismatch, report imbalance. At the end, the stack should be empty. Figures 1 and 2 show this method in action for balanced and non-balanced inputs, respectively.

Example with balanced brackets:

Figure 1: Example of a balanced bracket sequence detected using a stack.

Examples with non balanced brackets:

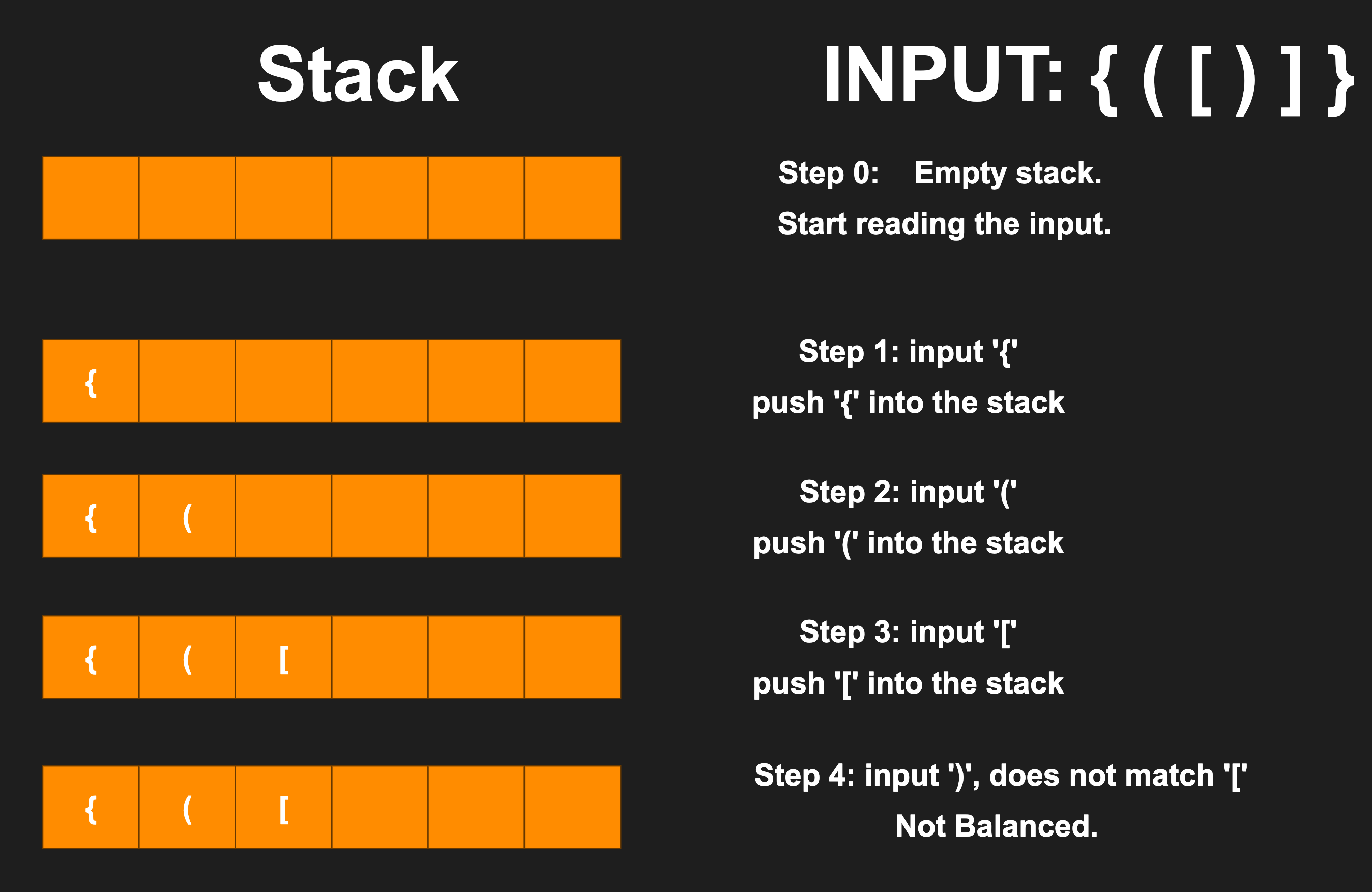
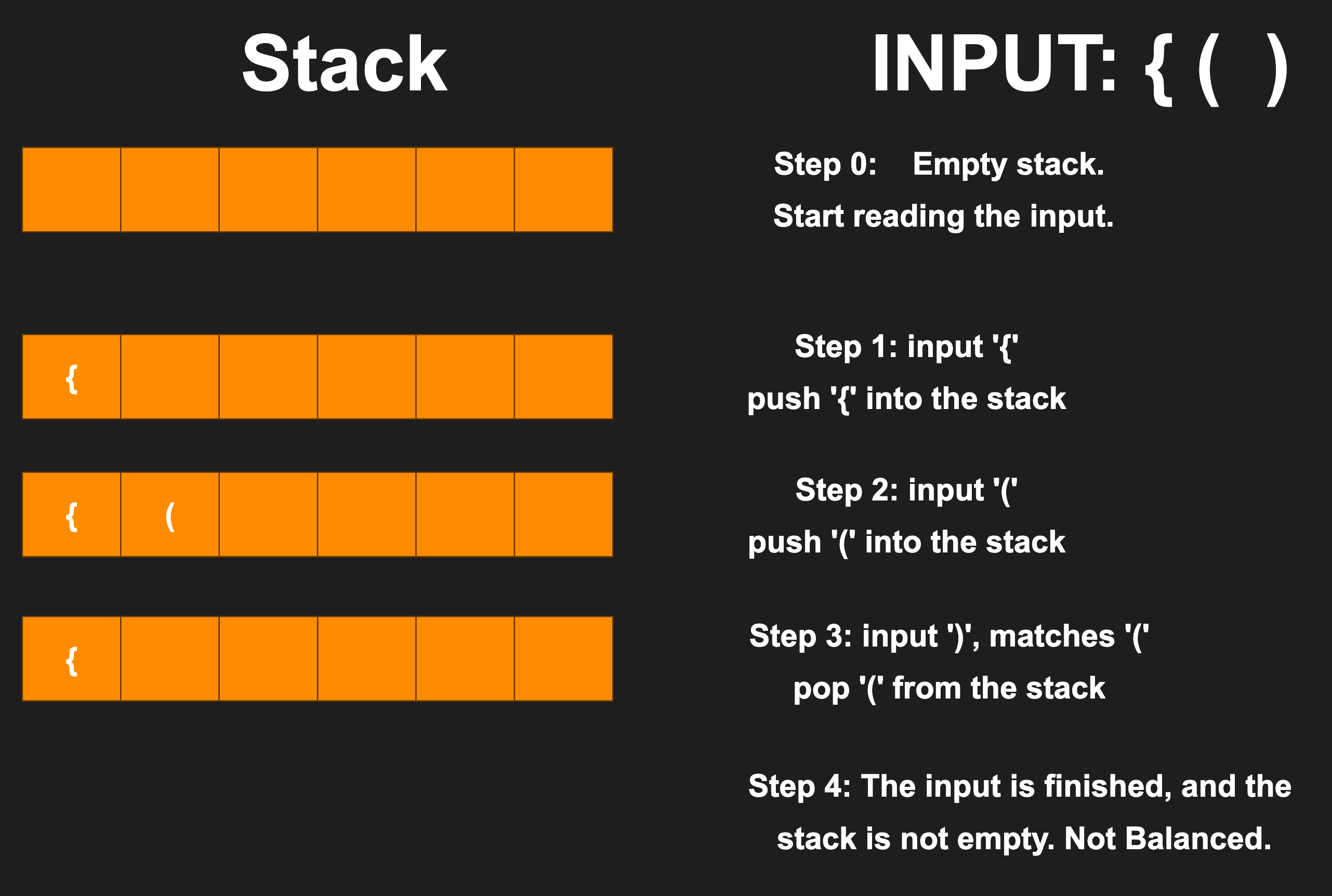
Figure 2: Examples of bracket sequences that are not balanced, detected using a stack.

Following is a more detailed description of the algorithm:

Balanced Brackets Algorithm

  1. Set up a Stack: Start with an empty stack to keep track of opening brackets.
  2. Go Through Each Character of the Input:
    • If the character is an opening bracket, like (, {, or [, push it into the stack.
    • If the character is a closing bracket, like ), }, or ], check two things:
      • If the stack is empty, return False (there’s no matching opening bracket).
      • If the stack isn’t empty, remove the top bracket from the stack and make sure it matches the closing bracket. If it doesn’t match, return False.
  3. Final Check: After going through all characters of the input, check if the stack is empty. If it’s empty, all brackets were balanced, so return True. If there’s anything left in the stack, return False.

Figure 3: A description of the algorithm using the list as a stack.

Code

Implement the algorithm from Figure 3 in the following function stub:

Test your code

Use the following main to test your function: