Binary Min-Heap

Introduction

A binary heap is a complete binary tree stored as a vector, where each parent node follows a specific order relation with its children. In a Min-Heap, the parent always has a smaller value than its children, ensuring efficient retrieval of the smallest element in \(O(\log N)\) time.

Binary heaps are widely used in:

Priority queues (e.g., scheduling tasks, network packet buffering)
Graph algorithms (e.g., Dijkstra’s shortest path)
Heap sort (efficient sorting algorithm)

Figure 1 below shows an example of a Min-Heap. See the caption for more detail.

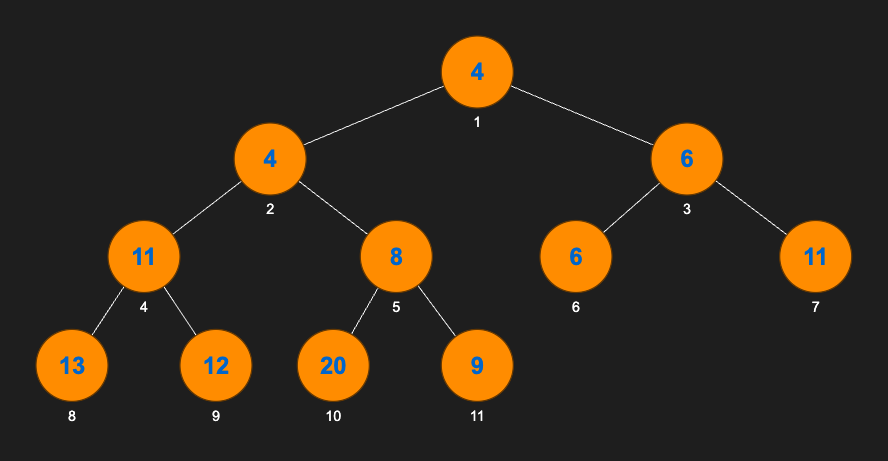
Figure 1: The tree interpretation of a binary Min-Heap. (Image created using yEd: https://www.yworks.com/products/yed/)

This tree in Figure 1 corresponds to the vector: [4, 4, 6, 11, 8, 6, 11, 13, 12, 20, 9].

Below each node in Figure 1 is the index of the value in that node in the corresponding vector. Note that indices begin from 1. This is a convention followed in theoretical descriptions of binary heaps.

Structure of the heap tree

The structure of the tree is encoded by three simple relationships, given below. For a given node \( i \), its left child is found at \( 2i \), the right child at \( 2i + 1 \), and the parent of \( i \) is found at \( \frac{i}{2} \).

\[ \text{Left child of } i: \quad 2i \] \[ \text{Right child of } i: \quad 2i + 1 \] \[ \text{Parent of } i: \quad \frac{i}{2} \]

The type of tree shown in Figure 1 is called a complete tree. This is a tree in which all levels, except possibly the last level, are full (i.e., they are not missing any nodes). The last level may not be full; however, the nodes in it must be aligned to the left, meaning there are no gaps between nodes.

Height of a complete binary tree

A perfect binary tree is a complete binary tree whose last level is full. The number of nodes \( N \) of a complete binary tree of height \( h \) (assuming \( h \geq 1 \)) can be bounded by the number of nodes in a perfect binary tree of height \( h-1 \) as follows:

\[ 2^0 + 2^1 + \ldots + 2^{h-1} < N \]

\[ \implies 2^h - 1 < N \]

\[ \implies h < \log_2(N + 1) \]

Hence, for a binary heap with \( N \) elements, the height of the heap tree is no more than \( \log_2(N + 1) \).

This implies that any heap operation that traverses a path in the tree has a time complexity proportional to \( \log_2(N) \).

The shape and order properties

A binary heap (in this case a Min-Heap) is required to maintain two properties at all times:

Shape property: The heap must always be a complete binary tree.
Order property: For any node \( i \), the value at \( i \) must be less than or equal to the values in its child nodes (if they exist), i.e., the nodes at \( 2i \) and \( 2i + 1 \). There is no order constraint among sibling nodes, however.

Task 1: Print the heap tree

As we implement a binary heap, it will be useful to be able to view the data in the vector as the logical heap tree. We need to write a function called printHeap to do this for us. Use the provided main to test your implementation.

Provide a full implementation for this function. The function should be able to print the heap in a format that, even though not completely tree-like, makes it easier to read the tree structure.

For example, for the vector: [4, 4, 6, 11, 8, 6, 11, 13, 12, 20, 9, 6, 19, 13] , the tree could be printed as:

[4]
[4,6]
[11,8][6,11]
[13,12][20,9][6,19][13]

The function prints one level per line. It uses square brackets to enclose siblings at each level (single values appear within brackets when they have no siblings) and siblings are separated by commas. There are no spaces.

Task 2: heapifyDown and heapifyUp

One of the fundamental operations required to maintain a binary min-heap is called heapify. Its task may be described as follows:

Given a binary min heap, of valid shape, and the values of all but one node \( i \) in the correct place according to the order property, move the value at \( i \) to its correct place according to the order property, while maintaining the shape of the heap.

In the context of heapify, the value at \( i \) may violate the order property in one of two possible ways: (1) the value at \( i \) is greater than the value of a child of \( i \), or (2) the value at \( i \) is smaller than its parent.

The method used to resolve (1) is called heapify down, and the method to resolve (2) is heapify up.

heapifyDown

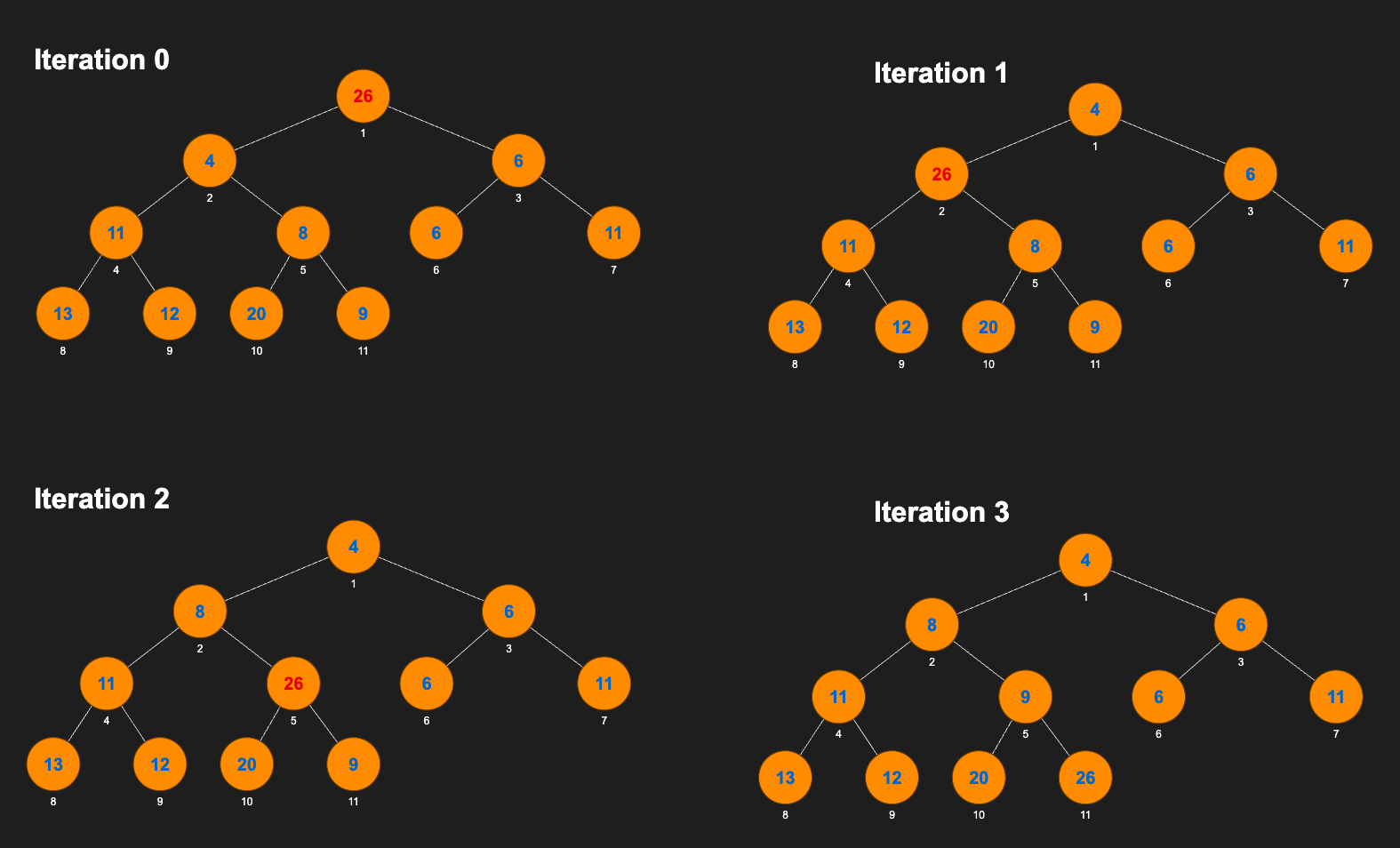
Figure 2 below shows the action of heapifyDown. We begin with a properly shaped heap in which one node, at the root in this case, contains a value that is greater than a child's value (both children's values in this case). The algorithm proceeds by moving this value down the heap, one level at a time, using the following rules:

Case 1: If the node at \( i \) has only one child \( j \), and the value at \( i \) is greater than the value at \( j \): swap the value at \( i \) with the value at \( j \). Set \( i \) to \( j \) and repeat.

Case 2: If the node at \( i \) has two children \( j \) and \( k \), and the value at \( j \) is less than or equal to the value at \( k \) and less than the value at \( i \): swap the value at \( i \) with the value at \( j \). Set \( i \) to \( j \) and repeat.

Case 3: If \( i \) has no children, or the value at \( i \) is less than or equal to the values at the children, STOP.

Figure 2: Shows heapifyDown in action. Starting with an invalid value at the root, namely 26, it is moved down the heap using the algorithm described in this section. (Image created using yEd: https://www.yworks.com/products/yed/)

heapifyUp

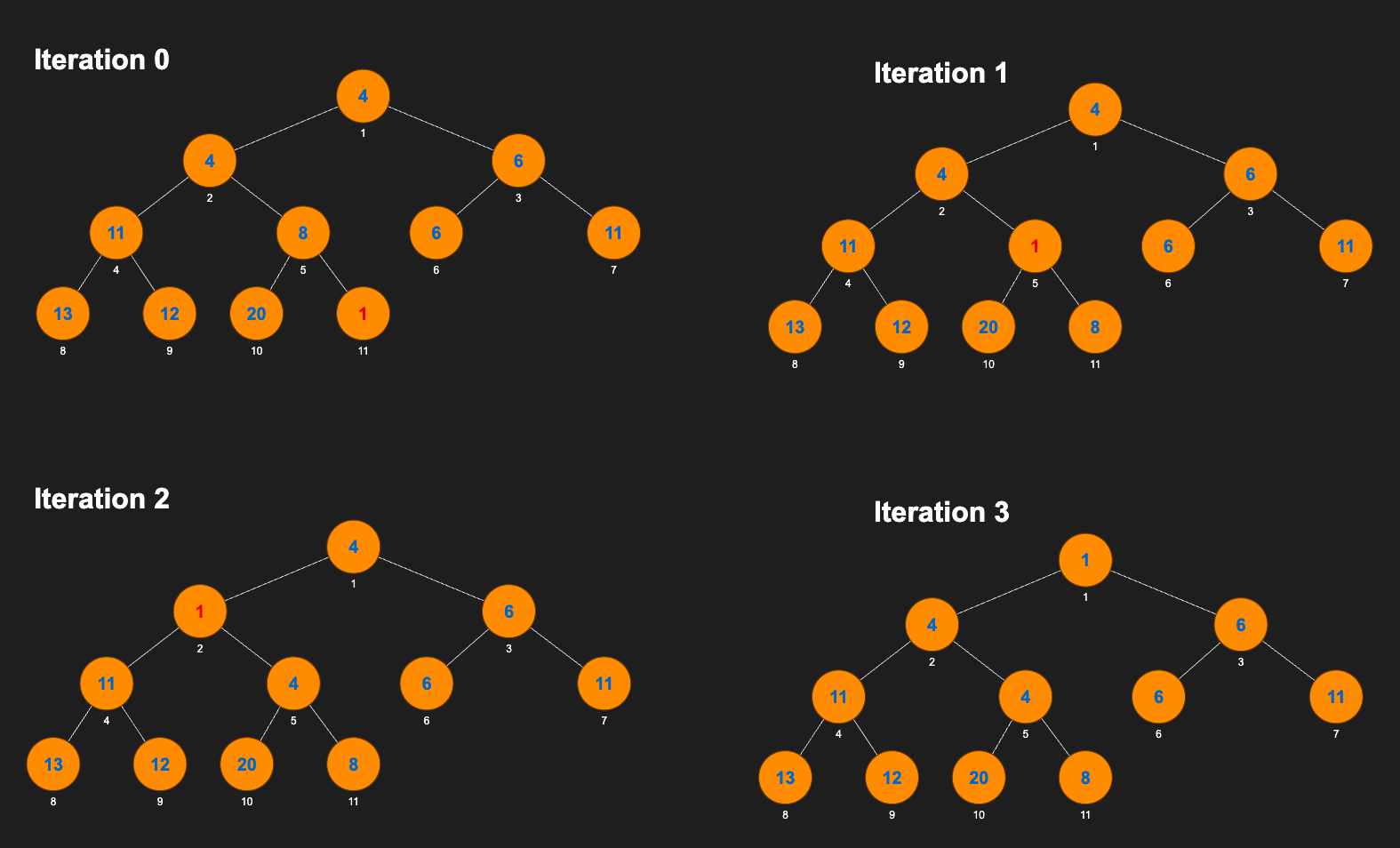
For heapifyUp, only two cases suffice:

Case 1: If the node at \( i \) has a parent \( p \) and the value at \( i \) is less than the value at \( p \), swap the values at \( i \) and \( p \). Set \( i \) to \( p \) and repeat.

Case 2: If node \( i \) has no parent or the value at \( i \) is greater than or equal to the value at the parent, STOP.

The action of heapifyUp is shown below in Figure 3.

Figure 3: Shows heapifyUp in action. In this case the value 1 violates the order property. The heapifyUp algorithm proceeds to move it up the tree until (in this case) it reaches the root. (Image created using yEd: https://www.yworks.com/products/yed/)

Implement and test heapifyDown and heapifyUp.

Task 3: insert, removeMin, and getMin

We should be able to insert new elements into the heap, remove the minimum element from the heap, and get the minimum element. Given the way the heap is designed, the last task is quite simple: simply return the value at the root.

For insert, the following algorithm suffices:

Push back the new element to the end of the vector (making it the rightmost node in the last level of the tree). Then, call the heapifyUp function on the newly added node.

For removeMin, the strategy is also simple. We note that the minimum element is at the root of the tree. We use the following algorithm:

Swap the value at the root with the value in the rightmost node in the last level (i.e., the value at index (size - 1) of the vector). Next, pop back the last element from the vector. Then, call heapifyDown on the root node.

Implement and test insert, removeMin, and getMin

Use the following main to test all functions.

Contents