Problem 4.4 Ghost Leg Permutation
Introduction
This is a competition problem, featured in the ICPC (International Collegiate Programming Contest) North America Qualifier, 2022.
A Ghost Leg is a method for representing permutations.
A Ghost Leg can be represented as a set of vertical lines, each line corresponding to one element of the set being permuted.
Horizontal lines (like the rungs of a ladder) connect adjacent vertical lines in such a way that no two rungs share an endpoint. An example is shown in the illustration in Figure 1.
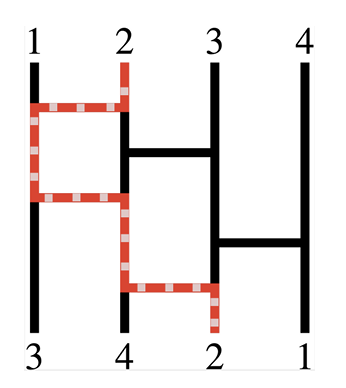
Tracing
To determine the resulting position of any element under a Ghost Leg permutation, begin at the top of the vertical line corresponding to that element. Trace a path down the line until encountering the first rung touching that line. Follow that rung to the adjacent vertical line. It does not matter whether the rung goes to the left or to the right, just follow it. Continue downward, following rungs, until reaching the bottom. This gives the final position of that element under the permutation.
In the example in Figure 1, element 2 ends up third in the permutation. The path is shown with red dotted lines. Likewise, element 1 ends up fourth, element 3 ends up first, and element 4 ends up second.
Problem Input and Output
Given a description of a Ghost Leg, determine the result of the permutation. In other words, apply the specified permutation, and output the elements in their permuted order.
Input
Read input from a file, input.txt.
The first line of input contains two positive integers \( n \) (\( 1 \leq n \leq 100 \)) and \( m \) (\( 0 \leq m \leq 1,000 \)), where \( n \) is the number of elements being permuted, and \( m \) is the number of rungs.
The vertical lines (elements) are identified from left to right by the integers \( 1 \) through \( n \). Each of the next \( m \) lines contains a single integer \( a \) (\( 1 \leq a < n \)), which indicates that there is a rung between vertical lines \( a \) and \( a + 1 \).
The rungs are listed in order from top to bottom of the Ghost Leg. Clearly, no two rungs can be at the same height.
Output
Output \( n \) lines, where each line contains a single integer. This is the resulting permutation. The first line is the element that ends up first in the permutation, the second is the element that ends up second, and so on.
Implementation
The following code contains an empty function (to be implemented by you), and a main that tests it.
Note: This problem does not require more than a couple of passes of the input.
Used these inputs: input1.txt, input2.txt, input3.txt