Problem 2.1 Large Spikeless Rectangles

This is a problem from image processing. We are processing black and white images. Each image is a two-dimensional grid. In this case, each pixel is either 1 (representing a black pixel) or 0 (representing a white pixel). We are interested in determining regions of black intensity. As operations like this one are frequently performed, we have done some preprocessing and mapped the two-dimensional image to a 1-dimensional list, called count. Each element in count contains the number of 1s in a row of the original image. More precisely, count[i] = the number of black pixels in row i of the image.

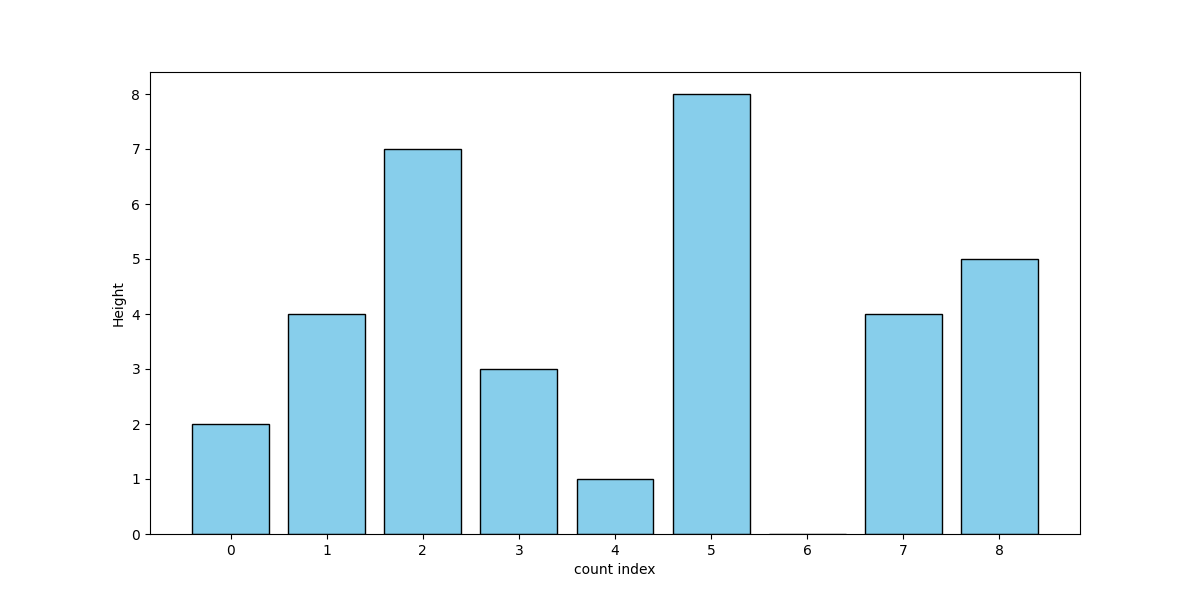
We can now visualize count as a bar graph. For example, if count = [2, 4, 7, 3, 1, 8, 0, 4, 5], then it can be visualized as in Figure 1 below.

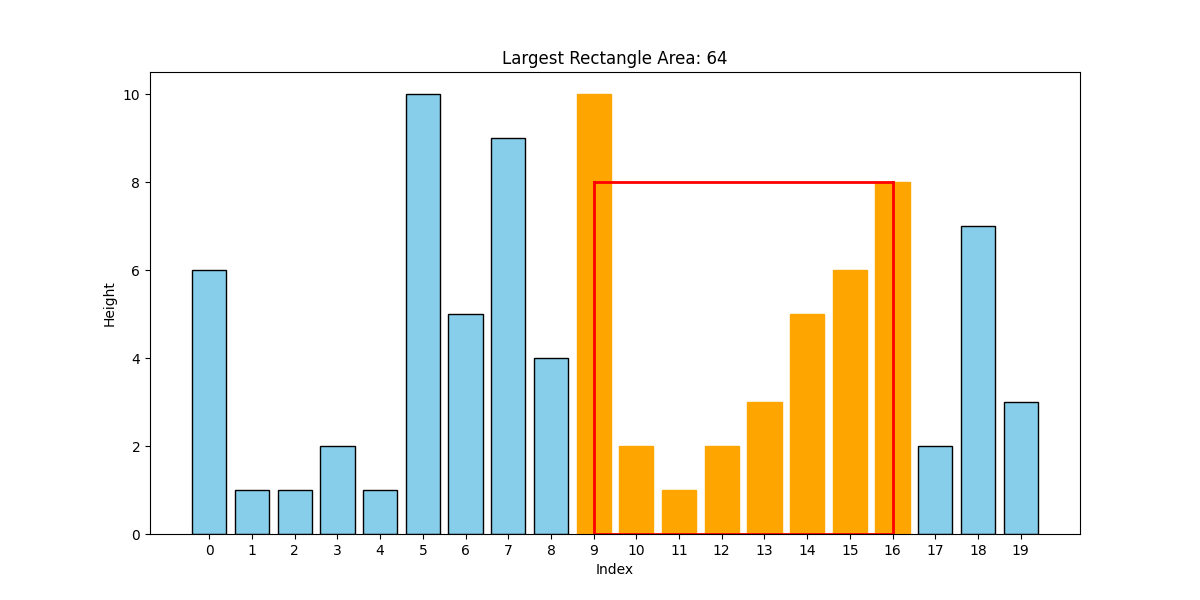
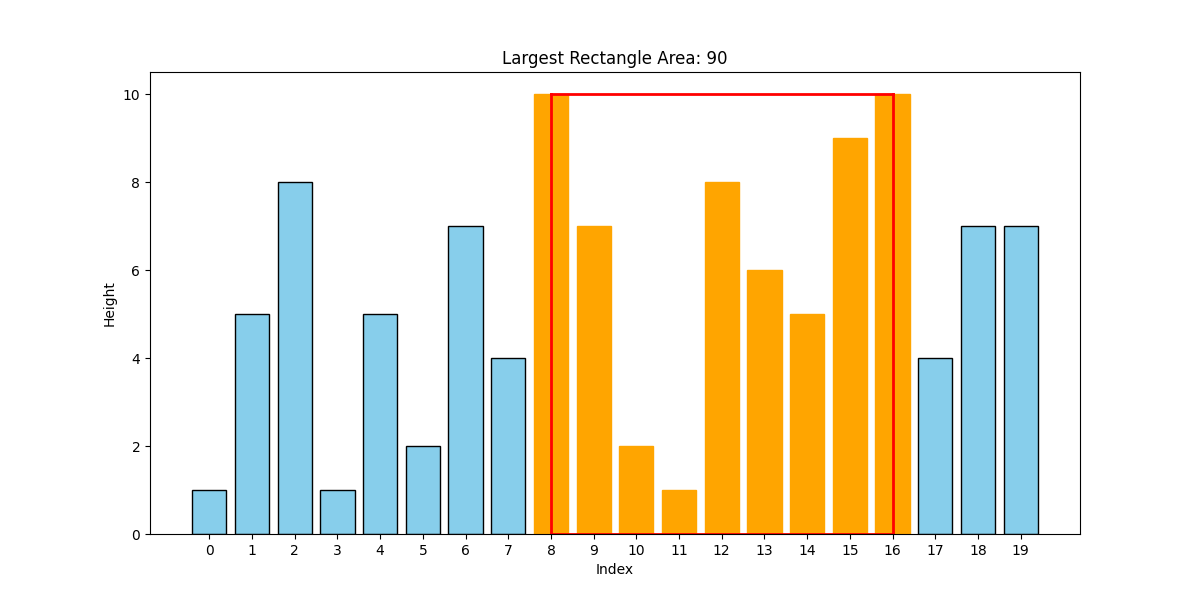
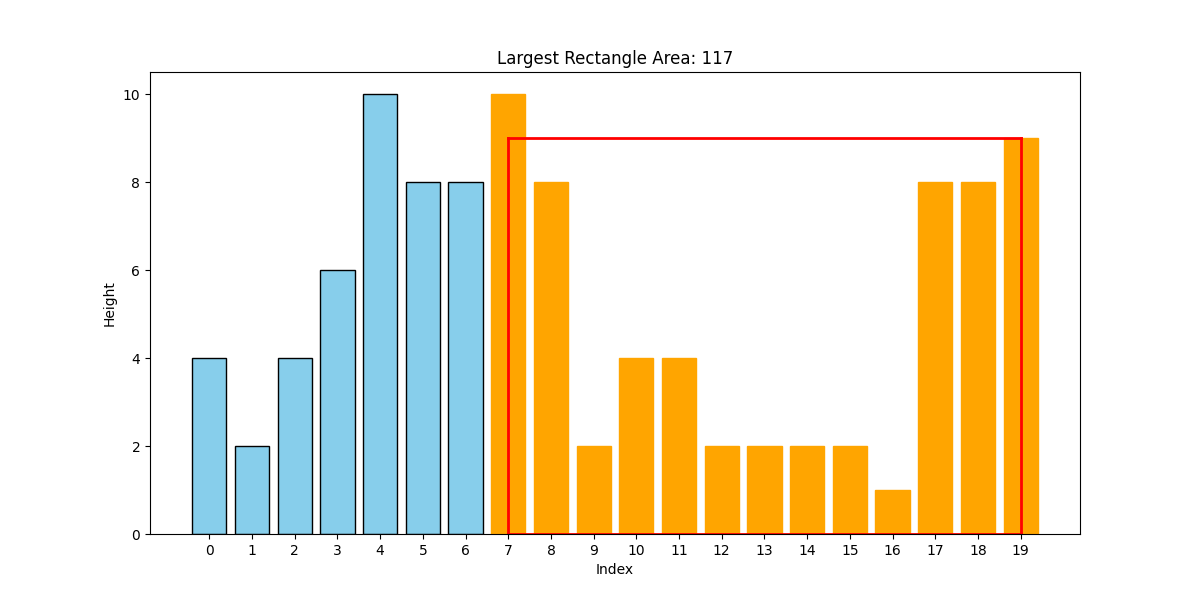
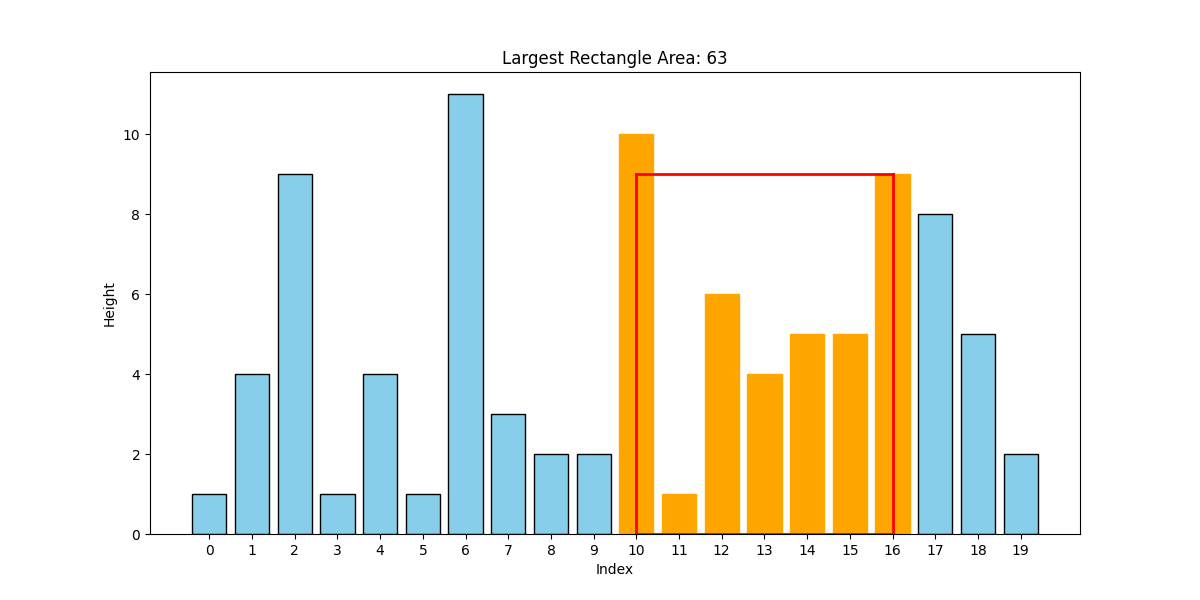
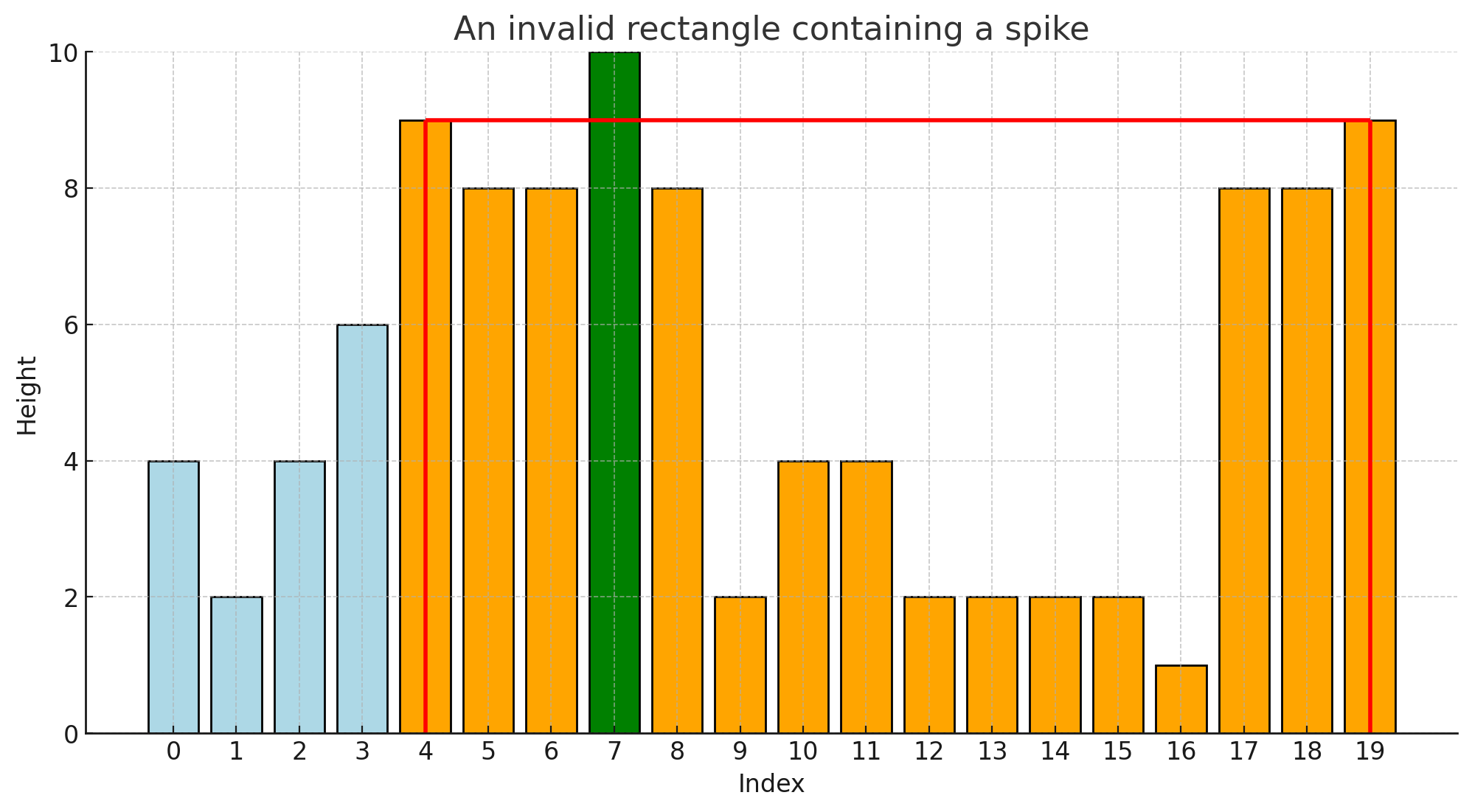
Figure 1: The 'count' list visualized as a bar graph. The height of bar i corresponds to the number of black pixels in row i of the image.

In order to detect areas of black intensity, we consider rectangles composed of the bars of this bar graph. Figure 2 shows four different examples of such rectangles (shown in red). Note that such a rectangle represents the black intensity within consecutive rows of the image. The area of such a rectangle provides an approximation of the black intensity of a region of the image (though not necessarily a rectangular region of the image).

Some terminology for rectangles

side bars: The bars making up the left and right sides of the rectangle. A single bar rectangle is also possible, in which case both its side bars are the same bar.

internal bars: The bars lying inside the rectangle (between the two side bars).

width: The number of bars in the rectangle, including both side and internal bars. (The width of each individual bar is taken to be 1).

height: The height of the shortest side bar of the rectangle. In case of a single bar rectangle, the height of that bar is the height of the rectangle.

area: The product the height and width of the rectangle.

spike: An internal bar that exceeds the height of the rectangle. Figure 3 shows an example of a rectangle with a spike (green bar).

spikeless rectangle: A rectangle that has no spikes. Four examples of spikeless rectangles are shown in Figure 2.

In this problem we are interested only in spikeless rectangles.

Figure 2: Four different examples of largest spikeless rectangles and their corresponding areas.

Figure 3: An example of a rectangle with a spike (green bar).

Python code

Given the list count, our goal is to find the spikeless rectangle with the largest area. Implement the following Python function for this purpose. In this version of the solution write a cubic time algorithm, i.e., an algorithm that takes approximately \( c \cdot N^3 \) time, where \( c > 0 \) is a constant and \( N \) is the size of the list. The algorithm will inspect each candidate rectangle, while ensuring that it is spikeless by traversing through its bars. The function should finally report the largest candidate rectangle. A utility function called updateMaxRectangle has been provided to you to use appropriately within your code.

Use the following main to test your function:

The quadratic time method

The aim now is to find the desired rectangle in quadratic time, i.e., approximately \( d \cdot N^2 \) time, where \( d > 0 \) is a constant and \( N \) is the size of the list. As before, you will need to check all candidate rectangles, however, to check whether a candidate rectangle is spikeless you should not need to traverse through all its bars again.

Implement the following function for the quadratic time method. You may use the same main as above to test your function by changing the name of the function being called in the main.

A faster method?

There is in fact a cnlgn (c>0) time solution to this problem, however, it uses a recursive technique and we shall return to it in due course.