Problem 2.2 Possibly Spiked Rectangles

Spikeless rectangles provide a reasonable approximation for high black intensity regions, but they have some limitations. For example, since the area of the rectangle is computed using its sides, rectangles with small internal bars may be selected, resulting in regions of the image that have low black intensity in the interior.

A better approach is to consider all rectangles, including those that may (or may not) contain spikes. Moreover, we modify the definition of the height of a rectangle as below.

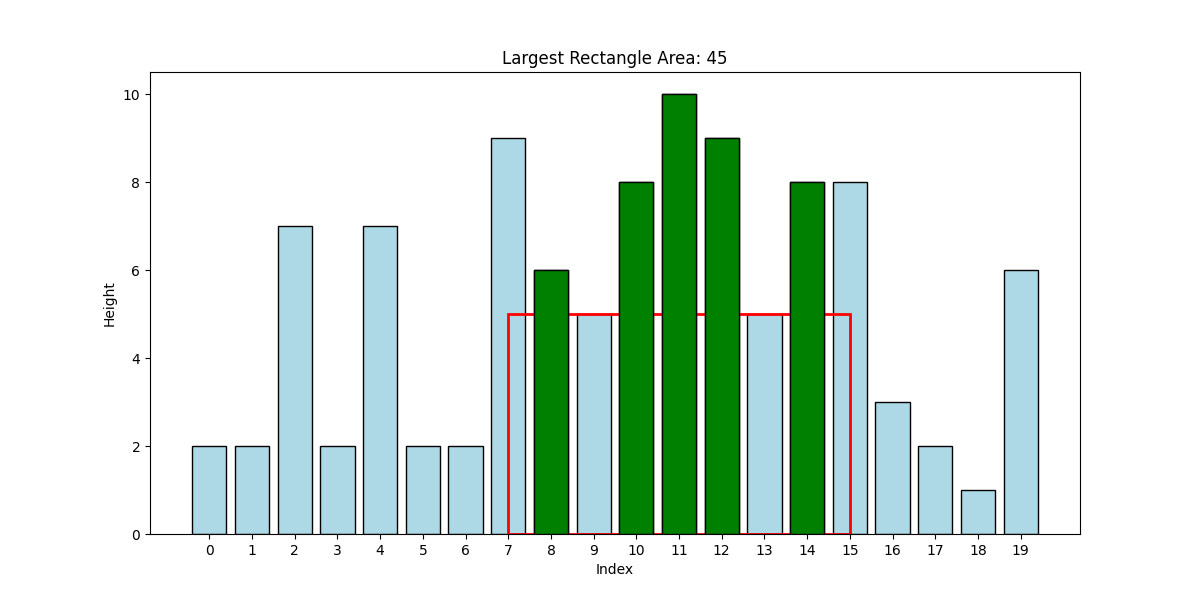
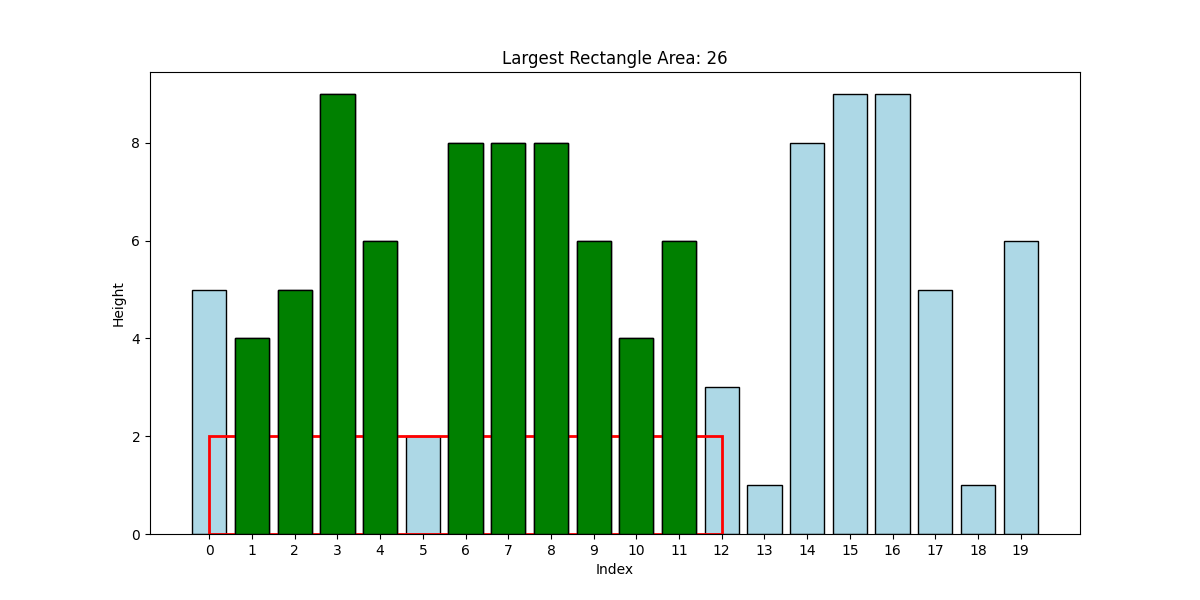
Height of a rectangle The height of a rectangle is the height of its shortest bar, which may be an internal or side bar.

Figure 1 below shows two examples of largest rectangles with spikes and their corresponding areas. Please note that although these examples show rectangles that do contain spikes, if a spikeless rectangle with larger area exists, it will be chosen as the largest rectangle. We simply do not need to check for spikelessness in this problem.

Figure 1: Two different examples of largest rectangles with spikes and their corresponding areas.

Python code

Our task is to write a quadratic time algorithm to compute the largest rectangle (which may or may not contain spikes). We will inspect all possible rectangles and do not need to check for spikelessness. However, be careful to use the height of the shortest bar as the height of the rectangle.

Implement the following Python function for this purpose:

Use the following main to test your function:

A linear time method?

There is in fact a linear time solution to this problem, however, it requires the use of a particular data structure and we shall return to it in due course.