Problem 3.1 Stock Analysis by Maximum Rise

We are writing a small piece of code to help analyze the rise of a stock price over a period of time to support investment decisions.

We are given time series data for the prices of a particular stock, represented as a list where each value is the stock price at a specific time point. The time points are represented by indices: 0, 1, 2, ... .

As an indicator of the potential of the stock to create profit, we wish to compute the maximum rise in its price between two time points.

Specifically, given a list \( prices \) of \( N \) time based price values, we want to find indices \( i \) and \( j \) (where \( 0 \leq i < j < N \)) such that \( prices[j] - prices[i] \) is the maximum among all possible \( i, j \) pairs.

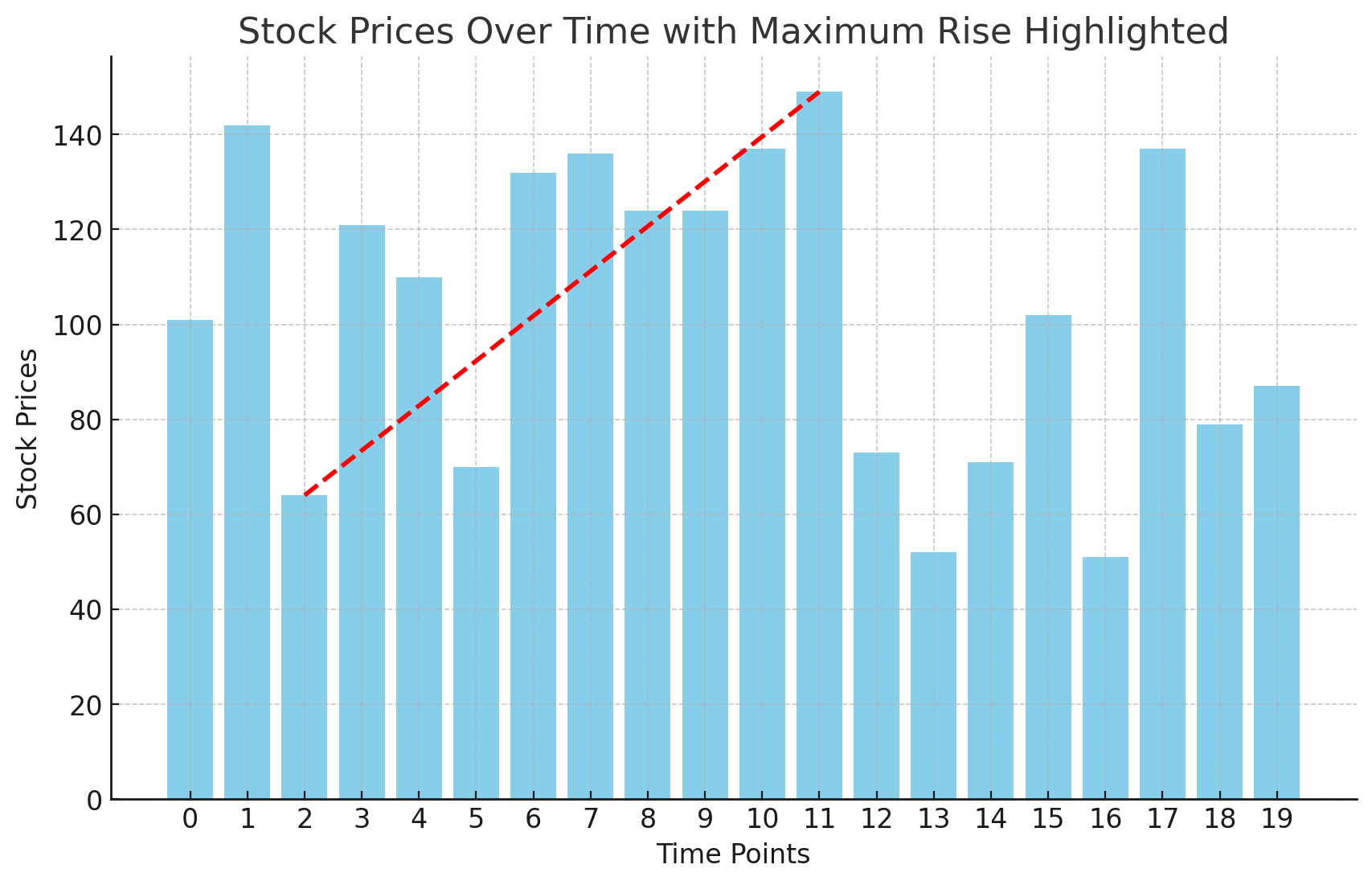
Figure 1 below shows the stock prices as blue bars, with the red dotted line indicating the maximum rise in price.

Figure 1: Visual representation of the time series price data and the maximum rise in price shown as a red dashed line.

Code

The simple method to compute the required indices checks all possible \( (i, j) \) pairs of indices and picks the one that results in the maximum rise. As a warm-up, implement the following function stub using this straightforward approach. Then, refine your method to ensure it makes only a single pass through the prices.

Note: if the prices do not show any rise (i.e., the prices continue to decrease or stay the same from start to end), the function should return the triple (-1, -1, -1) representing the fact that no valid rise was found.

Test your code

Use the following main to test your function: