← Back

Table of Contents

Introduction Implementation 1: Sorting by repeated selection Implementation 2: Sorting by digits

Problem 1.1 Sorting Binary Identifiers

Introduction

We consider a network server that receives binary identifiers in the form of \(0/1\) strings, each of length \(d\), from up to \(2^d\) communicating machines.

These identifiers may arrive in large quantities, often repeatedly from the same machine. To analyze the communication behavior of each machine effectively, it is important to first sort the received data by machine identifiers.

Sorting enables efficient organization of the data associated with the identifiers. This may further enable the server to detect patterns, count interactions, and identify anomalies or irregularities in communication behavior.

Problem definition

We are given a vector identifiers of \(N\) binary strings, where each string is of fixed length \(d\). The task is to sort the strings in non-decreasing order of the binary numbers they represent.

For example:

Input: identifiers = {"100", "110", "101", "110", "000", "101"}
Output: identifiers = {"000", "100", "101", "101", "110", "110"}

Important Notes:

  1. All strings in the vector identifiers have the same length \(d\).
  2. The number of identifiers, \(N\), can be any positive integer. (\(N\)is potentially much larger than \(d\)).
  3. The same identifier may repeat any number of times in identifiers.

Implementation 1: Sorting using repeated selection (slow)

One of the simplest sorting algorithms works as follows:

Sorting by Repeated Selection

Traverse through the elements (strings, in this case) of the vector, and for each element:

  • Find the smallest element from the current position to the end of the vector.
  • Swap the current element with the smallest element.

Let's begin by implementing this simple method in C++. The following code provides an empty sorting function (to be implemented by you), and a main that tests it.

Implementation 2: Sorting by digits, using auxiliary storage (fast)

This implementation sorts identifiers by exploiting their \(0/1\) structure.

It uses one digit position at a time as the sorting criterion.

The method is shown in Figure 1 below. Please take a careful look at how it works.

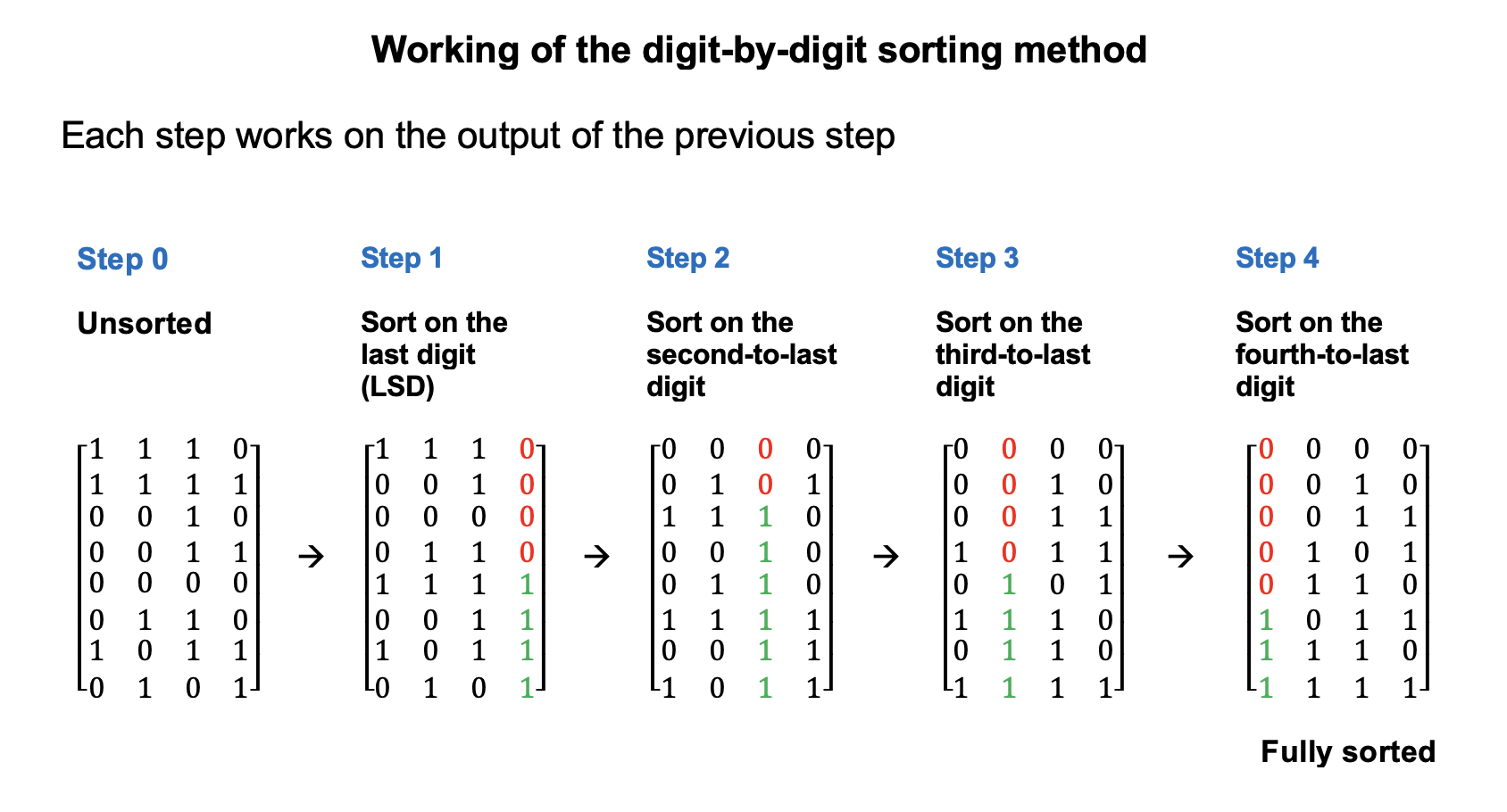
Figure 1: The working of the digit-by-digit sorting method. On each step, the output of the previous step is re-grouped based on the value of the next digit (moving from the least to most significant digit).

Following is a brief description of the method. The description is intentionally brief, and not all implementation details are provided. However, breaking the task into smaller functions can simplify the implementation.

A key point is that if two strings \(x\) and \(y\) have the same digit at any step, their relative order from the previous step must be preserved. This is critical for the method to work correctly.

Sorting Digit-by-Digit

Traverse through the \(d\) digit positions of the \(0/1\) strings from the least significant to the most significant digit position, and for each position:

  • Move all strings with a \(0\) at the current position before the strings with a \(1\) at the current position.
    • (In reordering strings, preserve the relative order of the strings that have the same digit (0 or 1) at the current position.)

Comparison: Repeated Selection vs. Digit-by-Digit Sorting

This comparison highlights how the digit-by-digit method is faster than repeated selection for sorting \(N\) identifiers (binary strings) of length \(d\).

The number of strings \(N\) is exponential in terms of \(d\), as there are \(2^d\) possible binary strings of length \(d\). Furthermore, strings can repeat, so \(N\) can greatly exceed \(2^d\), making \(N\) much larger than \(d\) in typical cases.

The repeated selection method takes time proportional to \(N^2 \cdot d\), as it repeatedly scans the unsorted portion of the strings to find the smallest, which involves comparing all pairs of strings.

The digit-by-digit method takes time proportional to \(d^2 \cdot N\). At each of the \(d\) digit positions, an additional cost of \(d \cdot N\) arises due to copying or processing the strings while grouping or rearranging them.

For example, consider sorting 1000 8-digit strings. The repeated selection method will require approximately \(N^2 \cdot d = 1000^2 \cdot 8 = 8,000,000\) basic operations. In contrast, the digit-by-digit method will require approximately \(d^2 \cdot N = 8^2 \cdot 1000 = 64,000\) basic operations, making it significantly faster.

The trade-off for the digit-by-digit method is the use of auxiliary storage to group strings during intermediate steps.

Finally, implement the digit-by-digit method in C++. The following code provides an empty sorting function (to be implemented by you). Use the same main as above to test your function.