Problem 1.3 Temperature Trends

As a data analyst for an environmental research company, you need to identify periods of sustained temperature increase from sensor data collected over time. This time, however, the focus is on detecting the longest trends of increasing temperatures. A trend is a sub-sequence of the input data, containing not necessarily contiguous readings, where each reading is higher than the previous one in the trend. A trend represents a sustained period of warming, capturing a general pattern that persists even amidst daily fluctuations (which could include noise). By identifying trends, researchers can gain insights into prolonged warming phases that may not be evident when only considering cumulative sums of temperature values (as sums could turn out to be high due to outliers, for example).

Your task is to determine the length of the longest, not necessarily contiguous, subsequence of increasing temperature readings from the data.

A Visual Example

The plots below show three different longest sequences of rising tempteratures detected from the same input. A longer rising trend is not present in this input. In our task, we are interested only in finding the length of this longest sequence, or trend, which in this case is 10.

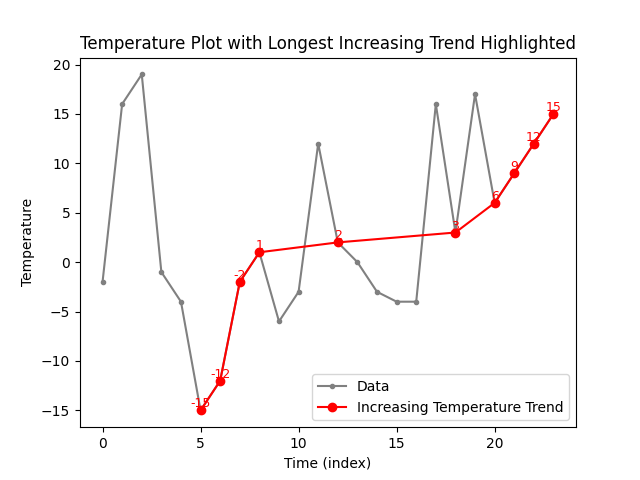
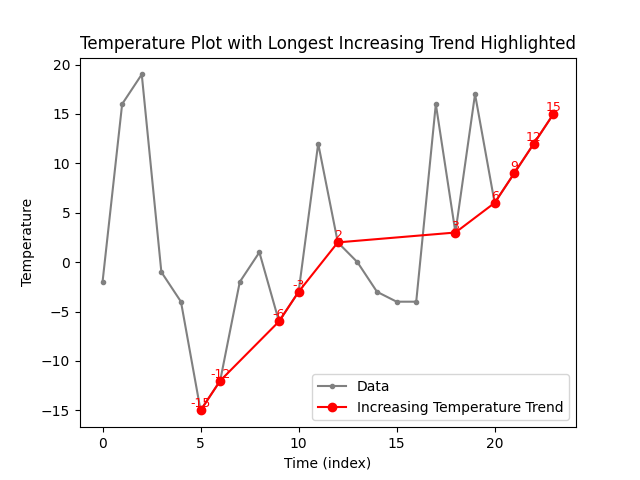
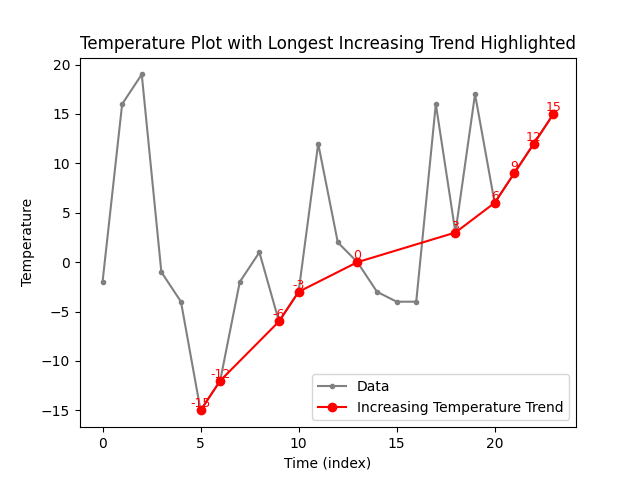
Figure 1: Plots show three different longest sequences of rising tempteratures detected from the same input. Each has length 10. Our program's output in this case should be 10: the length of the trend.

Further examples of inputs and outputs:

Some example inputs and their corresponding outputs are shown below:

Input: data = [5, 2, 8, 6, 3, 6, 9, 5]

Output: Longest trend length = 4

Explanation: The longest increasing trend is [2, 3, 6, 9], which has a length of 4.

Input: data = [1, 7, 3, 5, 9, 2, 8, 6]

Output: Longest trend length = 4

Explanation: The longest increasing trend is [1, 3, 5, 9], or [1, 3, 5, 8], or [1, 3, 5, 6], each of which has length 4.

Input: data = [3, 10, 2, 1, 20]

Output: Longest trend length = 3

Explanation: The longest increasing trend is [3, 10, 20], which has a length of 3.

How many possible trends are there?

A trend is essentially a subsequence of the input sequence. For an input sequence of length \( N \), i.e., it contains \( N \) numbers, the number of subsequences could be as large as \( 2^N \). This would be a prohibitively large number for any reasonably large value of \( N \). We need therefore to design a method to find the desired trend (in our case its length) without exhaustively searching through all \( 2^N \) possible subsequences.

Python code

Implement the following function stub:

Use the following main to test your function: